www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Bahas Soal Matematika » Limit ›
Hitunglah \( \displaystyle \lim_{x \to 0^+} \ x \ \ln x \).
Pembahasan:
Jika kita substitusi \(x = 0\) ke fungsi limitnya, kita peroleh bentuk tak tentu (0) (∞). Aturan L'Hospital tidak dapat diterapkan pada bentuk tak tentu berupa perkalian seperti itu, karena Aturan L'Hospital hanya berlaku pada bentuk tak tentu pembagian, misalnya 0/0 atau ∞/∞.
Akan tetapi, kita dapat memodifikasi fungsi limitnya sehingga diperoleh bentuk tak tentu pembagian. Perhatikan berikut ini:
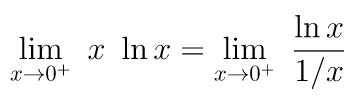
Sekarang, jika kita substitusi \(x = 0\) ke fungsi limit yang telah dimodifikasi ini, kita peroleh bentuk tak tentu ∞/∞ sehingga kita dapat menerapkan Aturan L'Hospital untuk menyelesaikan limit tersebut, yakni:

Jadi, hasil dari \( \displaystyle \lim_{x \to 0^+} \ x \ \ln x = 0 \).